Machine Learning

Getting Started

DeepLearning.TV YouTube playlist -- good starter!

Tuts

UFLDL Stanford (Deep Learning) Tutorial

Principles of training multi-layer neural network using backpropagation <-- Great visual guide!

Courses

Neural Networks for Machine Learning — Geoffrey Hinton, UToronto

- Coursera course
- Vids (on YouTube)
- same, better organized
- Intro vid for course
- Hinton's homepage
- Bayesian Nets Tutorial -- helpful for later parts of Hinton

Deep learning at Oxford 2015 (Nando de Freitas)

Notes for Andrew Ng's Coursera course.

Hugo Larochelle: Neural networks class - Université de Sherbrooke RESOURCES

Karpathy -- CS231n

Boltzmann Machines

Hopfield to Boltzmann http://haohanw.blogspot.co.uk/2015/01/boltzmann-machine.html which links to http://arxiv.org/pdf/1510.04781v2.pdf

Hinton's Lecture, then:

https://en.wikipedia.org/wiki/Boltzmann_machine

http://www.scholarpedia.org/article/Boltzmann_machine

Hinton (2010) -- A Practical Guide to Training Restricted Boltzmann Machines

https://www.researchgate.net/publication/242509302_Learning_and_relearning_in_Boltzmann_machines

Boltzmann Distribution

Consider this 'background'.

Suppose you have some system being held in thermal equilibrium by a heat-bath. Now suppose the system has a finite number of possible states. Like a 3x3x3 cm cube containing molecules with total KE 900J, and the states are: {first 1x1x1 zone has 999J, next has 1, others have 0} (very unlikely), {998,1,1,0,...}, etc. Notice we are making (two) artificial discretisation(s). So let's think of the whole cube as the reservoir/heat-bath and the middle 1x1x1 cm zone as our system. (better would be to make our reservoir much larger e.g. 101x101x101 in proportion to our system -- think infinite).

We would expect our system to fluctuate around 100J. We can ask: what is the probability our system has 97J at a given moment? Boltzmann figured out that if you know the energy of a particular state you can figure out the probability the system is in that state:

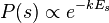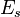$P(s)\propto e^{{-kE_{s}}}$ where $E_{s}$ is the energy for that state.

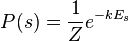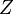So we can write: $P(s)={\frac {1}{Z}}e^{{-kE_{s}}}$ where $Z$ is the PARTITION FUNCTION (energy summed over all possible states).

If you graph the energy (X axis) vs probability {system has that energy} (Y axis) you have a Boltzmann Distribution.

Susskind derives this here.

Boltzmann MACHINE

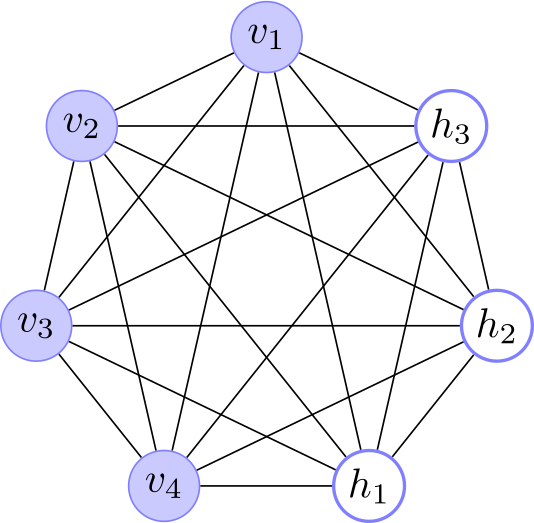
A Boltzmann Machine is a Hopfield Net, but each neuron stochastically has state 0 or 1.

So, imagine a 12 point mystic rose: 3 hidden units, 9 visible units. You can visualise the weights between each pair of units by the thickness of that line if you like.

Retrieval: First imagine the network is already trained, i.e. suppose weights are fixed in such a way that input vectors 111-000-000, 000-111-000 and 000-000-111 generate basins i.e. minima of low network energy (network energy is just the sum of active synapses. So 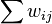$\sum w_{{ij}}$ where i,j both on).

So, set visible units to 111-100-000, set the 3 hidden units to random binary & keep randomly choosing a neuron and updating its state (0 or 1) by some probabilistic logic that will guarantee our system eventually settles down into a Boltzmann distribution, i.e. reaches thermal equilibrium.

This will mean that with high probability it will be in a low energy state. Think: place a marble nearby & it will roll to the nearest basin. So we should be able to recover 000-111-000.

Now let's cook up that updating logic.

It looks like Wikipedia's approach here is to suppose the system is already in a Boltzmann distribution & we wish to update it in a way that it is still in a Boltzmann distribution afterwards:

We can calculate the probability of a given unit's state being ON just by knowing the system's energy gap between that unit being ON and OFF:

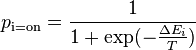$p_{{\text{i=on}}}={\frac {1}{1+\exp(-{\frac {\Delta E_{i}}{T}})}}$ where $\Delta E_{i}=E_{{\text{i=off}}}-E_{{\text{i=on}}}$

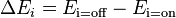
Yup that's a good ole Sigmoid! And it should be simple to get that Energy delta just by figuring out the expected Energy contribution of that neuron.

---

That demonstrates its retrieval ability. But how about its storage ability?

i.e. If you feed in those three training images, we need some way of twiddling the weights to create 3 appropriate basins. i.e. We want the network to have ultralow energy for those 3 input vectors.

So you want to perform some kind of gradient descent: figure out the rate at which the energy is decreasing as you twiddle your weight. And adjust the weight to get maximum energy decrease.

Hinton describes this process on Scholarpedia: Learning in Boltzmann machines.

${\bigg \langle }{\frac {\partial \log P({\mathbf {v}})}{\partial w_{{ij}}}}{\bigg \rangle }_{{\mathrm {data}}}=\langle s_{i}s_{j}\rangle _{{\mathrm {data}}}-\langle s_{i}s_{j}\rangle _{{\mathrm {model}}}=\Delta$

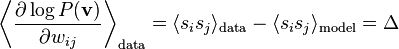
Actually is there a simpler way to think of this? The RHS is just the elevation of synapse-load (for this particular synapse) (or 'fire-together' if you like) during training over the same during 'dreaming'. So we want to 'wire-together' in proportion to 'fire together'. This is good ole Hebbian Learning.

Now since 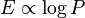$E\propto \log P$, we have 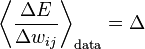${\bigg \langle }{\frac {\Delta E}{\Delta w_{{ij}}}}{\bigg \rangle }_{{\mathrm {data}}}=\Delta$ which we can write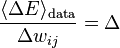 ${\frac {\langle \Delta E\rangle _{{\mathrm {data}}}}{\Delta w_{{ij}}}}=\Delta$

i.e. 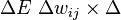$\Delta E~\Delta w_{{ij}}\times \Delta$ ... struggling to finish this.

---

Papers

Applying Deep Learning To Enhance Momentum Trading Strategies In Stocks

- Hinton, Salakhutdinov (2006) -- Reducing the Dimensionality of Data with Neural Networks

Books

Nielsen -- Neural Networks and Deep Learning <-- online book

http://www.deeplearningbook.org/

https://page.mi.fu-berlin.de/rojas/neural/ <-- Online book

The Elements of Statistical Learning

S/W

http://playground.tensorflow.org

TensorFlow in IPython YouTube (5 vids)

SwiftNet <-- My own back propagating NN (in Swift)

Stats Courses

OxEduc: Bayesian statistics: a comprehensive course

Gibbs Sampling -- Niemi

Misc

Oxford AI/Trader

Links: https://github.com/memo/ai-resources

http://colah.github.io/posts/2014-03-NN-Manifolds-Topology/ <-- Great article!

http://karpathy.github.io/2015/05/21/rnn-effectiveness/

https://www.youtube.com/watch?v=gfPUWwBkXZY <-- Hopfield vid

http://www.gitxiv.com/ <-- Amazing projects here!