Difference between revisions of "Machine Learning"

From PiWiki
Jump to: navigation, search
(→‎Boltzmann Machines)
(→‎Boltzmann Machines)
Line 28: Line 28:
 
=== Boltzmann Machines ===
 
=== Boltzmann Machines ===
  
−
Boltzmann Distribution connects the probability of a system being in a certain state with the energy of that state: <math>P(s) \propto e^{-kE_s}</math> where <math>E_s</math> is the energy for that state.
+
Hopfield to Boltzmann http://haohanw.blogspot.co.uk/2015/01/boltzmann-machine.html
  
−
So we can write: <math>P(s) = \frac{1}{Z}e^{-kE_s}</math> where <math>Z</math> is the PARTITION FUNCTION (energy summed over all possible states).  Reversing we can write <math>E_s = -\frac{1}{k} ln(Z P(s))</math>
+
Hinton's Lecture, then:
  
−
IIUC there is a wide class of systems that settle down into a Boltzmann distribution.
+
https://en.wikipedia.org/wiki/Boltzmann_machine
  
−
Each (binary) vector of unit-outputs creates a corresponding Energy state. Let's assume these energy states form a Boltzmann distribution.
+
http://www.scholarpedia.org/article/Boltzmann_machine
  
−
Then we can calculate the probability of a given unit's state being ON just by knowing the system's energy gap between that unit being ON and OFF: <math>p_\text{i=on} = \frac{1}{1+\exp(-\frac{\Delta E_i}{T})}</math> where <math>\Delta E_i = E_\text{i=off} - E_\text{i=on}</math> (working [https://en.wikipedia.org/wiki/Boltzmann_machine#Probability_of_a_unit.27s_state here])
+
[http://www.cs.toronto.edu/~hinton/absps/guideTR.pdf Hinton (2010) -- A Practical Guide to Training Restricted Boltzmann Machines]
  
−
Yup that's a good ole Sigmoid!
+
https://www.researchgate.net/publication/242509302_Learning_and_relearning_in_Boltzmann_machines
  
−
So if you seed your network with a random input vector (10001010110...), keep choosing random nodes & updating them using the above probability logic, eventually it should settle into a (locally)maximally probable state.
+
==== [https://en.wikipedia.org/wiki/Boltzmann_distribution Boltzmann Distribution] ====
 +
Suppose you have some system being held in thermal equilibrium by a heat-bath. Now suppose the system has a finite number of possible states. Like a 3x3x3 cm cube containing molecules with total KE 900J, and the states are: {first 1x1x1 zone has 999J, next has 1, others have 0} (very unlikely), {998,1,1,0,...}, etc. Notice we are making (two) artificial discretisation(s).  So let's think of the whole cube as the reservoir/heat-bath and the middle 1x1x1 cm zone as our system. (better would be to make our reservoir much larger e.g. 101x101x101 in proportion to our system -- think infinite).
  
−
So, let's say you want it to recognise 3 particular shapes: 111 000 000, 000 111 000 and 000 000 111.  If it's weights are set up just right, and you throw in 001 111 000, it should converge to 000 111 000 -- as the closest local energy basin.
+
We would expect our system to fluctuate around 100J.  We can ask: what is the probability our system has 97J at a given moment?  Boltzmann figured out that if you know the energy of a particular state you can figure out the probability the system is in that state:
  
−
That demonstrate its ''retrieval'' ability. But how about its '''storage''' ability?
+
:<math>P(s) \propto e^{-kE_s}</math> where <math>E_s</math> is the energy for that state.
  
−
i.e. If you feed in those three training images, we need some way of twiddling the weights to create 3 appropriate basins.
+
So we can write: <math>P(s) = \frac{1}{Z}e^{-kE_s}</math> where <math>Z</math> is the PARTITION FUNCTION (energy summed over all possible states).
  
−
-----
+
If you graph the energy (X axis) vs probability {system has that energy} (Y axis) you have a '''Boltzmann Distribution'''.
  
−
Think: Hopfield Net, but each neuron stochastically has state 0 or 1. Prob(state <- 1) = sigma(-z) where z = preactivation.
+
Susskind derives this [https://www.youtube.com/watch?v=SmmGDn8OnTA here].
  
−
Boltzmann distribution: [https://en.wikipedia.org/wiki/Boltzmann_distribution Wikipedia] [https://www.youtube.com/watch?v=SmmGDn8OnTA Susskind lecture]
+
Reversing we can write <math>E_s = -\frac{1}{k} \log(Z P(s)) = k_1 + k_2 \log P(s)</math>
  
−
Hopfield to Boltzmann http://haohanw.blogspot.co.uk/2015/01/boltzmann-machine.html
+
==== How is this useful? ====
  
−
Hinton's Lecture, then:
+
A Boltzmann Machine is a Hopfield Net, but each neuron stochastically has state 0 or 1.  Randomly update neurons: Prob(state sets to 1) = sigma(-z) where z = preactivation (sum of weighted inputs).
  
−
https://en.wikipedia.org/wiki/Boltzmann_machine
+
This is one of a wide class of systems that settle down into a Boltzmann distribution.
  
−
http://www.scholarpedia.org/article/Boltzmann_machine
+
Suppose weights are fixed. Each (binary) vector of unit-states creates a corresponding Energy state.  Let's assume these energy states form a Boltzmann distribution.
  
−
[http://www.cs.toronto.edu/~hinton/absps/guideTR.pdf Hinton (2010) -- A Practical Guide to Training Restricted Boltzmann Machines]
+
Then we can calculate the probability of a given unit's state being ON just by knowing the system's energy gap between that unit being ON and OFF: <math>p_\text{i=on} = \frac{1}{1+\exp(-\frac{\Delta E_i}{T})}</math> where <math>\Delta E_i = E_\text{i=off} - E_\text{i=on}</math> (working [https://en.wikipedia.org/wiki/Boltzmann_machine#Probability_of_a_unit.27s_state here])
  
−
https://www.researchgate.net/publication/242509302_Learning_and_relearning_in_Boltzmann_machines
+
Yup that's a good ole Sigmoid!
 +
 
 +
So if you seed your network with a random input vector (10001010110...), keep choosing random nodes & updating them using the above probability logic, eventually it should settle into a (locally)maximally probable state.
 +
 
 +
So, let's say you want it to recognise 3 particular shapes: 111 000 000, 000 111 000 and 000 000 111.  If it's weights are set up just right, and you throw in 001 111 000, it should converge to 000 111 000 -- as the closest local energy basin.
 +
 
 +
That demonstrate its ''retrieval'' ability. But how about its '''storage''' ability?
 +
 
 +
i.e. If you feed in those three training images, we need some way of twiddling the weights to create 3 appropriate basins. i.e. We want the network to have ultralow energy for those 3 input vectors.
 +
 
 +
-----
  
 
== Papers ==  
 
== Papers ==  

Revision as of 10:25, 27 August 2016

Getting Started

DeepLearning.TV YouTube playlist -- good starter!

Tuts

UFLDL Stanford (Deep Learning) Tutorial

Principles of training multi-layer neural network using backpropagation <-- Great visual guide!


Courses

Neural Networks for Machine Learning — Geoffrey Hinton, UToronto 

- Coursera course
- Vids (on YouTube)
- same, better organized
- Intro vid for course
- Hinton's homepage
- Bayesian Nets Tutorial -- helpful for later parts of Hinton

Deep learning at Oxford 2015 (Nando de Freitas)

Notes for Andrew Ng's Coursera course.

Hugo Larochelle: Neural networks class - Université de Sherbrooke

Karpathy -- CS231n

Boltzmann Machines

Hopfield to Boltzmann http://haohanw.blogspot.co.uk/2015/01/boltzmann-machine.html

Hinton's Lecture, then:

https://en.wikipedia.org/wiki/Boltzmann_machine

http://www.scholarpedia.org/article/Boltzmann_machine

Hinton (2010) -- A Practical Guide to Training Restricted Boltzmann Machines

https://www.researchgate.net/publication/242509302_Learning_and_relearning_in_Boltzmann_machines

Boltzmann Distribution

Suppose you have some system being held in thermal equilibrium by a heat-bath. Now suppose the system has a finite number of possible states. Like a 3x3x3 cm cube containing molecules with total KE 900J, and the states are: {first 1x1x1 zone has 999J, next has 1, others have 0} (very unlikely), {998,1,1,0,...}, etc. Notice we are making (two) artificial discretisation(s). So let's think of the whole cube as the reservoir/heat-bath and the middle 1x1x1 cm zone as our system. (better would be to make our reservoir much larger e.g. 101x101x101 in proportion to our system -- think infinite).

We would expect our system to fluctuate around 100J. We can ask: what is the probability our system has 97J at a given moment? Boltzmann figured out that if you know the energy of a particular state you can figure out the probability the system is in that state:

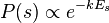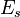P(s)\propto e^{{-kE_{s}}} where E_{s} is the energy for that state.

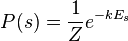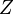So we can write: P(s)={\frac {1}{Z}}e^{{-kE_{s}}} where Z is the PARTITION FUNCTION (energy summed over all possible states).

If you graph the energy (X axis) vs probability {system has that energy} (Y axis) you have a Boltzmann Distribution.

Susskind derives this here.

Reversing we can write 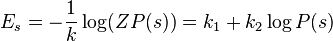E_{s}=-{\frac {1}{k}}\log(ZP(s))=k_{1}+k_{2}\log P(s)

How is this useful?

A Boltzmann Machine is a Hopfield Net, but each neuron stochastically has state 0 or 1. Randomly update neurons: Prob(state sets to 1) = sigma(-z) where z = preactivation (sum of weighted inputs).

This is one of a wide class of systems that settle down into a Boltzmann distribution.

Suppose weights are fixed. Each (binary) vector of unit-states creates a corresponding Energy state. Let's assume these energy states form a Boltzmann distribution.

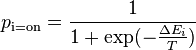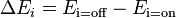Then we can calculate the probability of a given unit's state being ON just by knowing the system's energy gap between that unit being ON and OFF: p_{{\text{i=on}}}={\frac {1}{1+\exp(-{\frac {\Delta E_{i}}{T}})}} where \Delta E_{i}=E_{{\text{i=off}}}-E_{{\text{i=on}}} (working here)

Yup that's a good ole Sigmoid!

So if you seed your network with a random input vector (10001010110...), keep choosing random nodes & updating them using the above probability logic, eventually it should settle into a (locally)maximally probable state.

So, let's say you want it to recognise 3 particular shapes: 111 000 000, 000 111 000 and 000 000 111. If it's weights are set up just right, and you throw in 001 111 000, it should converge to 000 111 000 -- as the closest local energy basin.

That demonstrate its retrieval ability. But how about its storage ability?

i.e. If you feed in those three training images, we need some way of twiddling the weights to create 3 appropriate basins. i.e. We want the network to have ultralow energy for those 3 input vectors.

Papers

Applying Deep Learning To Enhance Momentum Trading Strategies In Stocks 

- Hinton, Salakhutdinov (2006) -- Reducing the Dimensionality of Data with Neural Networks


Books

Nielsen -- Neural Networks and Deep Learning <-- online book

http://www.deeplearningbook.org/

https://page.mi.fu-berlin.de/rojas/neural/ <-- Online book

S/W

http://playground.tensorflow.org

TensorFlow in IPython YouTube (5 vids)

SwiftNet <-- My own back propagating NN (in Swift)

Misc

Oxford AI/Trader

Links: https://github.com/memo/ai-resources

http://colah.github.io/posts/2014-03-NN-Manifolds-Topology/ <-- Great article!

http://karpathy.github.io/2015/05/21/rnn-effectiveness/

https://www.youtube.com/watch?v=gfPUWwBkXZY <-- Hopfield vid

http://www.gitxiv.com/ <-- Amazing projects here!

Retrieved from "http://pipad.org/wiki/index.php?title=Machine_Learning&oldid=190"