Difference between revisions of "Machine Learning"
(→Boltzmann Machines) |
(→Boltzmann Machines) |
||
| Line 36: | Line 36: | ||
Each (binary) vector of unit-outputs creates a corresponding Energy state. Let's assume these energy states form a Boltzmann distribution. | Each (binary) vector of unit-outputs creates a corresponding Energy state. Let's assume these energy states form a Boltzmann distribution. | ||
| − | + | Then we can calculate the probability of a given unit's state being ON just by knowing the system's energy gap between that unit being ON and OFF: <math>p_\text{i=on} = \frac{1}{1+\exp(-\frac{\Delta E_i}{T})}</math> where <math>\Delta E_i = E_\text{i=off} - E_\text{i=on}</math> (working [https://en.wikipedia.org/wiki/Boltzmann_machine#Probability_of_a_unit.27s_state here]) | |
| + | |||
| + | Yup that's a good ole Sigmoid! | ||
| + | |||
| + | So if you seed your network with a random input vector (10001010110...), keep choosing random nodes & updating them using the above probability logic, eventually it should settle into a (locally)maximally probable state. | ||
| + | |||
| + | So, let's say you want it to recognise 3 particular shapes: 111 000 000, 000 111 000 and 000 000 111. If it's weights are set up just right, and you throw in 001 111 000, it should converge to 000 111 000 -- as the closest local energy basin. | ||
| + | |||
| + | That demonstrate its ''retrieval'' ability. But how about its '''storage''' ability? | ||
| + | |||
| + | i.e. If you feed in those three training images, we need some way of twiddling the weights to create 3 appropriate basins. | ||
----- | ----- | ||
Revision as of 15:42, 26 August 2016
Getting Started
DeepLearning.TV YouTube playlist -- good starter!
Tuts
UFLDL Stanford (Deep Learning) Tutorial
Principles of training multi-layer neural network using backpropagation <-- Great visual guide!
Courses
Neural Networks for Machine Learning — Geoffrey Hinton, UToronto
- Coursera course - Vids (on YouTube) - same, better organized - Intro vid for course - Hinton's homepage - Bayesian Nets Tutorial -- helpful for later parts of Hinton
Deep learning at Oxford 2015 (Nando de Freitas)
Notes for Andrew Ng's Coursera course.
Hugo Larochelle: Neural networks class - Université de Sherbrooke
Boltzmann Machines
Boltzmann Distribution connects the probability of a system being in a certain state with the energy of that state: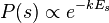 
where 
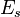is the energy for that state.
So we can write: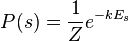 
where 
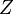is the PARTITION FUNCTION (energy summed over all possible states). Reversing we can write 
IIUC there is a wide class of systems that settle down into a Boltzmann distribution.
Each (binary) vector of unit-outputs creates a corresponding Energy state. Let's assume these energy states form a Boltzmann distribution.
Then we can calculate the probability of a given unit's state being ON just by knowing the system's energy gap between that unit being ON and OFF: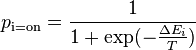 
where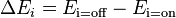 
(working here)
Yup that's a good ole Sigmoid!
So if you seed your network with a random input vector (10001010110...), keep choosing random nodes & updating them using the above probability logic, eventually it should settle into a (locally)maximally probable state.
So, let's say you want it to recognise 3 particular shapes: 111 000 000, 000 111 000 and 000 000 111. If it's weights are set up just right, and you throw in 001 111 000, it should converge to 000 111 000 -- as the closest local energy basin.
That demonstrate its retrieval ability. But how about its storage ability?
i.e. If you feed in those three training images, we need some way of twiddling the weights to create 3 appropriate basins.
Think: Hopfield Net, but each neuron stochastically has state 0 or 1. Prob(state <- 1) = sigma(-z) where z = preactivation.
Boltzmann distribution: Wikipedia Susskind lecture
Hopfield to Boltzmann http://haohanw.blogspot.co.uk/2015/01/boltzmann-machine.html
Hinton's Lecture, then:
https://en.wikipedia.org/wiki/Boltzmann_machine
http://www.scholarpedia.org/article/Boltzmann_machine
Hinton (2010) -- A Practical Guide to Training Restricted Boltzmann Machines
https://www.researchgate.net/publication/242509302_Learning_and_relearning_in_Boltzmann_machines
Papers
Applying Deep Learning To Enhance Momentum Trading Strategies In Stocks
- Hinton, Salakhutdinov (2006) -- Reducing the Dimensionality of Data with Neural Networks
Books
Nielsen -- Neural Networks and Deep Learning <-- online book
http://www.deeplearningbook.org/
https://page.mi.fu-berlin.de/rojas/neural/ <-- Online book
S/W
http://playground.tensorflow.org
TensorFlow in IPython YouTube (5 vids)
SwiftNet <-- My own back propagating NN (in Swift)
Misc
Links: https://github.com/memo/ai-resources
http://colah.github.io/posts/2014-03-NN-Manifolds-Topology/ <-- Great article!
http://karpathy.github.io/2015/05/21/rnn-effectiveness/
https://www.youtube.com/watch?v=gfPUWwBkXZY <-- Hopfield vid
http://www.gitxiv.com/ <-- Amazing projects here!
